数据分析：描述性统计术语汇总

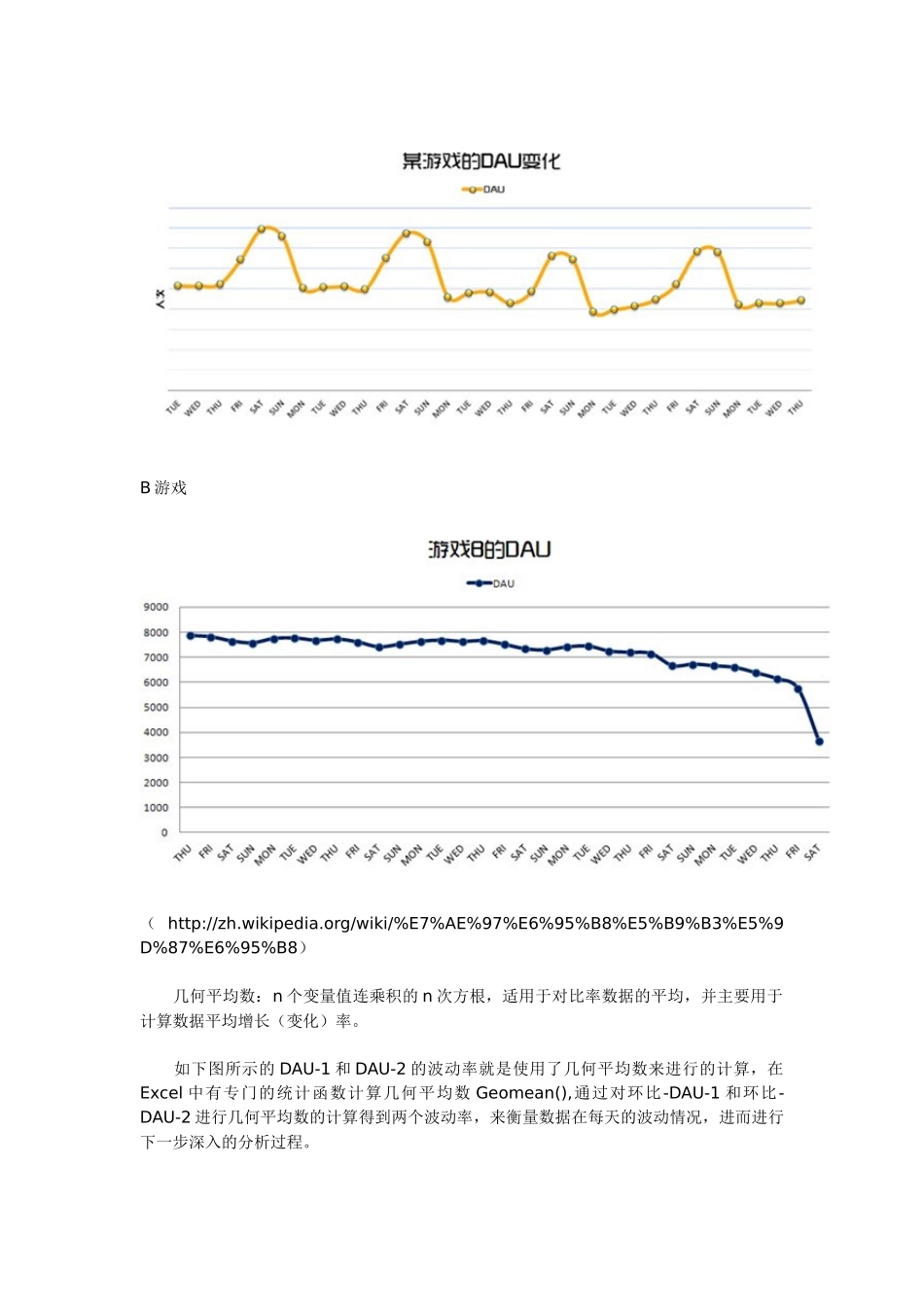
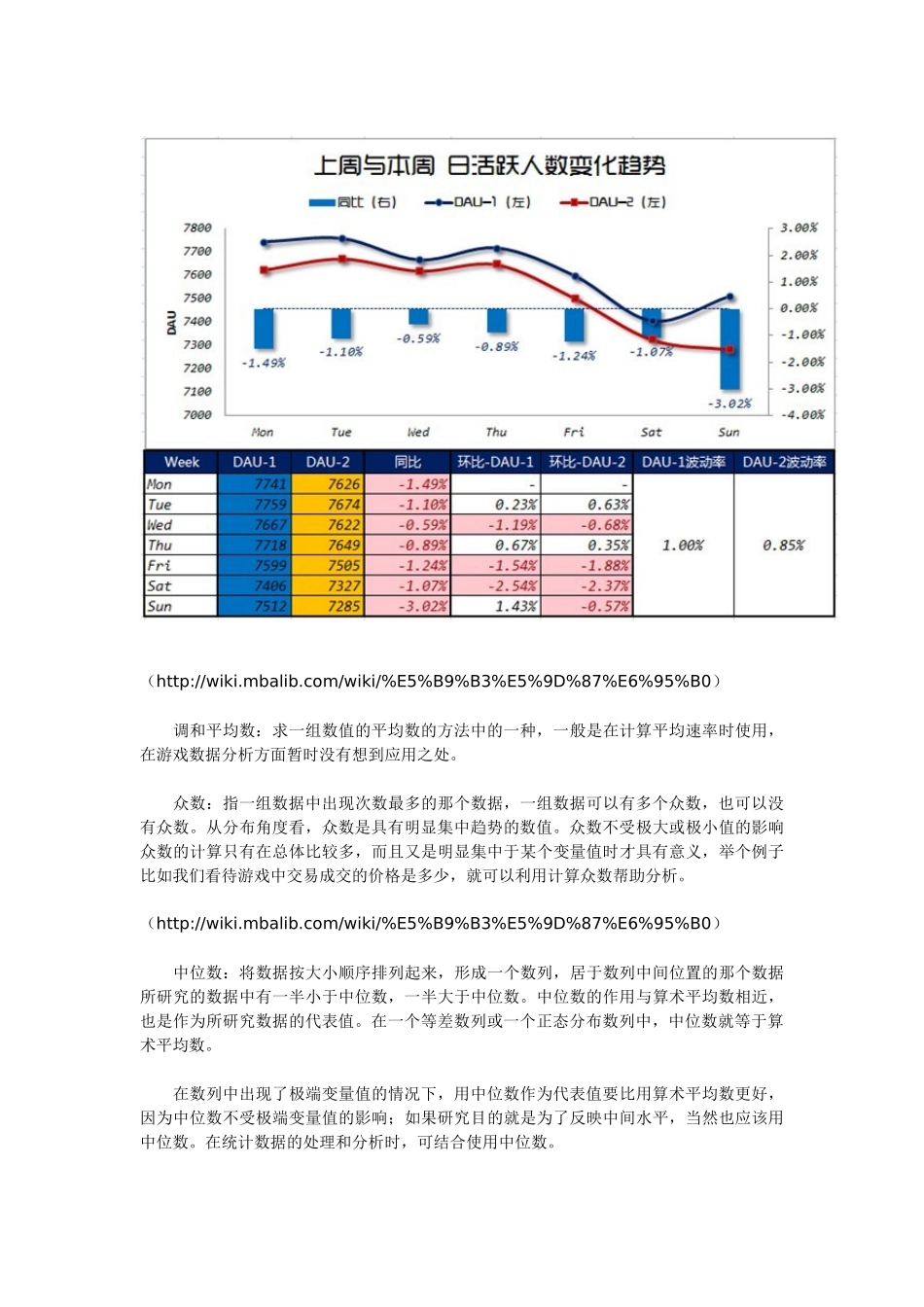
数据分析师不能仅仅靠着对数据的一种感觉和敏感来进行数据分析，这样的主观性太强，在合理必要的情况下，使用前人已经总结和使用的方法往往对我们更有帮助，但也要记住不要陷入这个指标误区中，核心还在于人（但不是让你凭感觉作分析），在于人对待问题的思考方式，解决办法。 今天来说说描述性统计分析，统计性描述分析是作为统计分析的第一步，在日常的数据分析中其实我们经常使用一些特征值，尤其是我们做周报或者月报的分析时，这些描述性的统计分析特征值对于我们有一定的帮助，描述性统计分析是进行正确的统计推断的先决条件。通过数据的分布类型和特点、集中和离散程度可进行初步分析。 鄙人经常使用 Excel 或者 SPSS 进行描述性的统计分析，描述性的统计分析包括数据收集、整理、显示，对数据信息的初步提取分析，在 SPSS 中我们有专门的描述性分析，其中涉及了很多的统计量，今天就索性把这些都列出来，给大家参考学习一下，需要说明的是这里列出来的不代表你就必须使用这些统计量，还是要根据业务的需要，适当的选取参考的统计量指标，这些指标是帮助我们分析数据异动，变化的“工具”，但请不要陷入指标的误区，每个指标的使用都是有一定的适用范围，大家需谨慎使用。 集中趋势：平均数（算数平均数、几何平均数、调和平均数、算术-几何平均数、平均数不等式）、众数、中位数等。 离散程度：全距、内距、平均差、标准误、离散系数等。 分布：偏态系数、峰度系数，反映数据偏离正态分布的程度。 下面为大家解释一下这些统计量，知识源于 MBALIB、百度百科、wiki。 首先来看平均数，平均数是统计学最常用的统计量，用于表示各观测值相对集中较多的中心位置，可以说是对数据集中趋势的反映，通常情况下初学者容易把平均数认为一组数据之和除以该组数据的个数，其实这样认识是有一定问题的，严格来说，平均数包括算数平均数、几何平均数、调和平均数、众数和中位数。具体的来看一下每个平均数的定义适用范围。 算数平均数：各观测值的总和除以观测值个数所得的商，简称平均数或均数，在统计学上的优点就是它较中位数、众数更少受到随机因素影响，缺点是它更容易受到极端数影响。比如在游戏日活跃人数方面，不同的游戏的活跃波动幅度是不同的，有的游戏会出现明显的异动和极值情况，比如一周内，周五、周六和周日的日活跃和 PCU 非常高，那么我们在计算这一周 7 天的平均日活跃时最好是不要计算一周的算数平均数，当然波动幅度不是非常大还是可以使用的，如下图所示的两款游戏的日活跃曲线，A 游戏最好分开计算周末和平日的日活跃，B 游戏则不需要分开计算。A 游戏B 游戏（ http://zh.wikipedia.org/wiki/%E7%AE%97%E6%95%B8%E5%B9%B3%E5%9D%87%E6%95%B8） 几何平均数：n 个变量值连乘积的 n 次方根，适用于对比率数据的平均，并主要用于计算数据平均增长（变化）率。 如下图所示的 DAU-1 和 DAU-2 的波动率就是使用了几何平均数来进行的计算，在Excel 中有专门的统计函数计算几何平均数 Geomean(),通过对环比-DAU-1 和环比-DAU-2 进行几何平均数的计算得到两个波动率，来衡量数据在每天的波动情况，进而进行下一步深入的分析过程。（http://wiki.mbalib.com/wiki/%E5%B9%B3%E5%9D%87%E6%95%B0） 调和平均数：求一组数值的平均数的方法中的一种，一般是在计算平均速率时使用，在游戏数据分析方面暂时没有想到应用之处。 众数：指一组数据中出现次数最多的那个数据，一组数据可以有多个众数，也可以没有众数。从分布角度看，众数是具有明显集中趋势的数值。众数不受极大或极小值的影响众数的计算只有在总体比较多，而且又是明显集中于某个变量值时才具有意义，举个例子比如我们看待游戏中交易成交的价格是多少，就可以利用计算众数帮助分析。（http://wiki.mbalib.com/wiki/%E5%B9%B3%E5%9D%87%E6%95%B0） 中位数：将数据按大小顺序排列起来，形成一个数列，居于数列中间位置的那个数据所研究的数据中有一半小于中位数，一半大于中位数。中位数的作用与算术平均数相近，也是作为所研究数据的代表值。在一个等差数列或一个正态分布数...